Calculate the mutual information between two vectors.

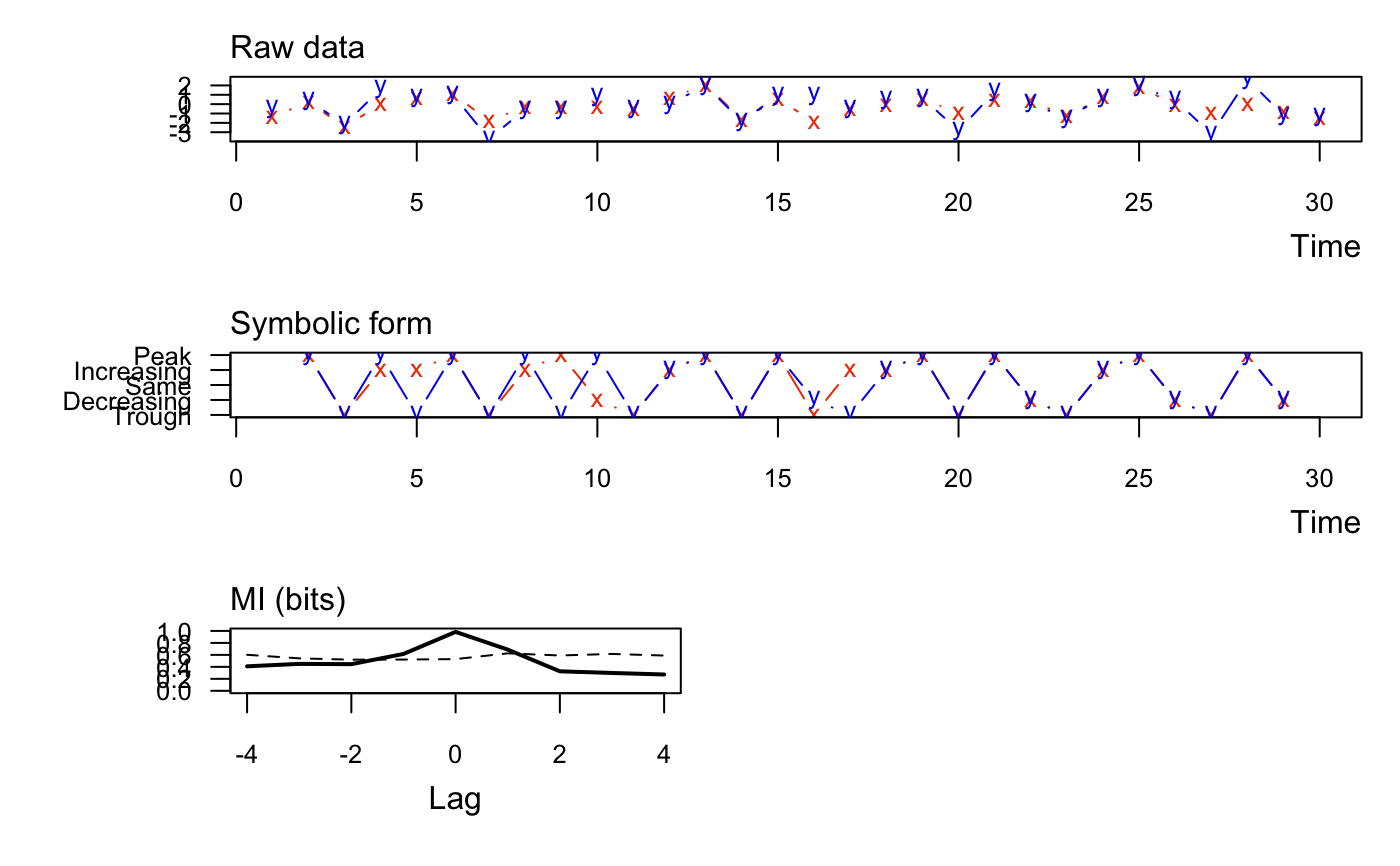
muti calculates the mutual information between two vectors at multiple lags and plots the results.

muti(x, y, sym = TRUE, n_bins = NULL, normal = FALSE, lags = seq(-4, 4),
  mc = 100, alpha = 0.05)

Arguments

x	First vector of data. Must be integer or numeric.
y	Second vector of data. Must be integer or numeric.
sym	Logical indicator of whether to use symbolic representation of the data when calculating the MI. If FALSE, the data are discretized based on n_bins.
n_bins	The number of bins to use for discretizing the data when sym = FALSE. When n_bins = NULL (default), the data are discretized based on the Rice rule where n_bins = ceiling(2*length(x)^(1/3)).
normal	Logical indicator of whether to normalize the mutual information to [0,1].
lags	One or more integers indicating at what lags to calculate the MI. Note that a negative (positive) lag means x leads (trails) y.
mc	The number of Monte Carlo simulations for estimating the critical threshold value on the mutual information, above which the MI is significant at the specified `alpha`. Must be a non-negative integer.
alpha	The alpha value for estimating the upper (1-alpha)% critical threshold on the mutual information.

Value

A data.frame with columns for lag (lag), mutual information between x & y (MI_xy), and the threshold value (MI_tv) above which the MI is signficant at the specified alpha. Note that the lower bound for MI is 0. Also returns plots of x & y (top panel), their discrete values (middle panel), and the mutual information at specified lags (bottom panel).

Examples

TT <- 30
x <- rnorm(TT)
y <- x + rnorm(TT)
muti(x, y)
#>   lag MI_xy MI_tv
#> 1  -4 0.409 0.602
#> 2  -3 0.450 0.542
#> 3  -2 0.445 0.520
#> 4  -1 0.615 0.522
#> 5   0 0.984 0.530
#> 6   1 0.688 0.626
#> 7   2 0.326 0.590
#> 8   3 0.298 0.616
#> 9   4 0.272 0.589